Schematic Diagram

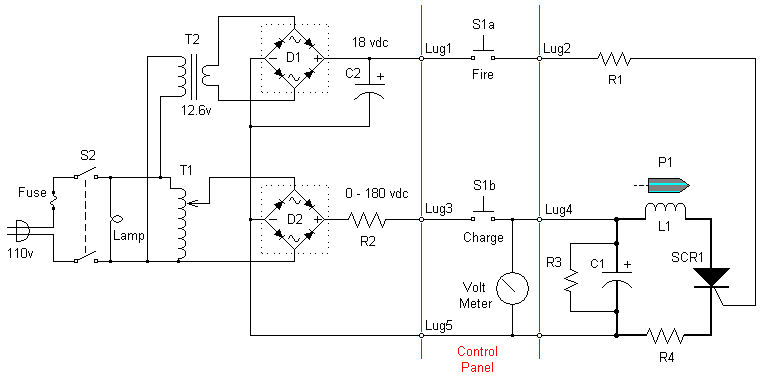
Parts List

C1 – 12,000 uF 200wvdc
C2 – 15 uF 25wvdc
D1 – 800v bridge rectifier
D2 – 800v bridge rectifier
L1 – coil, 56 turns 12 AWG
P1 – iron projectile
R1 – 220 ohm 1 watt
R2 – 25 ohm 25 watt
R3 – 150K ohm 1 watt
R4 – 62 milliohm 5 watt
S1 – momentary action DPDT center-off switch
S2 – DPST power switch
SCR1 – stud-type SCR, GE C158N, 800v 110-amp
T1 – Variac transformer, 0-132 volts, 6-amp
T2 – 12.6 vac filament transformer, 0.45-amp
Lamp – 110v panel indicator
Fuse – 110v 5A fuse
Meter – 0-200 vdc volt meter

Note that a Variac does not provide line isolation, for which you must not connect grounded equipment or an oscilloscope! T1 can be replaced with a fixed-voltage transformer for line isolation.

Terminal Strip Lugs

The lugs bracketed in the schematic as "control panel" are the connection point from the power supplies to the switches and coilgun. The lugs have advantages over soldered connections. They simplify testing, provide connection points for meters, and allow easy replacement of a power source. For example, an 18v battery pack with 160v inverter could replace the transformers with the simple use of a screwdriver.

The lugs are numbered 1 through 5 from top to bottom, as shown in this photograph.